Figure 5: It is an elliptic curve.
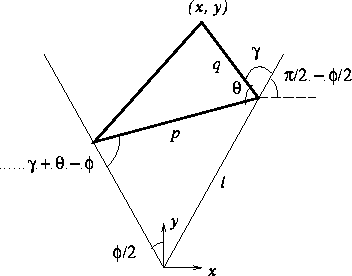
Given two locators and their corresponding edges, the part can move while maintaining the two point contact. During the motion, the third edge in consideration sweeps out a region within which it can achieve the third point contact. This motion is difficult to characterize and the region swept out by the third edge has a complicated shape. To simplify the analysis, we can instead consider the motion of the triangle, formed by the three point locators, in the moving frame attached to the moving part. The triangle's two vertices can slide on two edges of the part, while the third vertex sweeps out a curve in the moving frame. If this curve in the moving frame intersects the third edge, there exists a two-dimensional rigid body motion to achieve three point contact. Note that all three edges are now fixed edges in the moving frame. Now the question becomes: what is that curve in the moving frame?
To characterize the curve swept out by the third locator, we assume,
without loss of generality, that the triangle is sliding on a cone,
which has its apex at the origin and is symmetric about y-axis (Figure
5). Furthermore, given the cone and the triangle, the
following values are constants: 
, p, 
and q. The
position (x, y) of the third vertex of the triangle is uniquely
determined by a single parameter 
. Zhuang and Goldberg
[1997] shows in detail that this curve is an
elliptic curve:
where
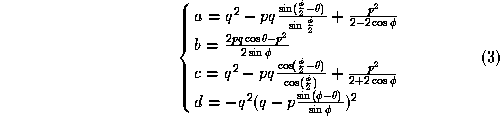
We call this curve the contact locus for design. The detail of a similar derivation of the elliptic curve can be found in [Jia and Erdmann, 1996].