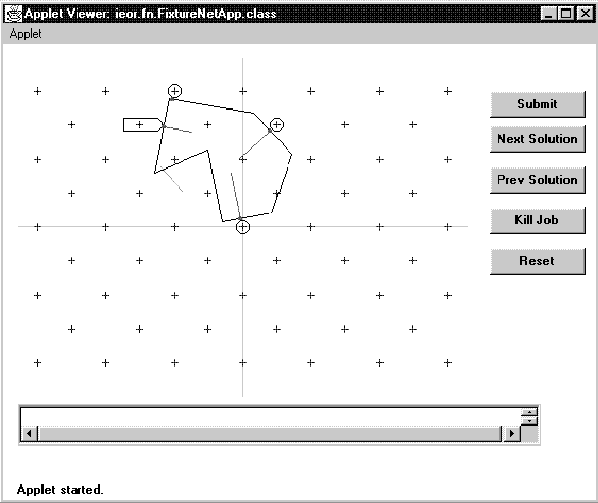
Figure 3: Screen shot showing a part, the fixture, the
user-specified force, and the reaction forces.
Once we have a fixture from FixtureNet, we may wish to study the effects of forces applied to the part such as force that will result when the part is machined while in the fixture. When a force is applied, the fixels will resist the force. These are the reaction forces we wish to study.
In preparation for displaying the reaction forces, the applet must compute the contact point of the fixels with the edges. Although the FixtureNet server obviously has this information, it is not communicated back to the client - a common problem when dealing with legacy systems. Therefore, we must calculate it from the information provided. This is difficult because the FixtureNet server supports fixels with non-zero diameters. This means that fixels do not lie directly on an edge, but rather a small distance from it.
We reverse-engineer this information by trying every pair of edge and fixel. We compute the distance from the fixel to the edge. For each fixel, we keep track of the closest edge we have found. When we are done with the enumeration, we have four edges paired with the four fixels. Note, that it is possible for two fixels to be located on the same edge.
For a given fixel, once we know which edge it contacts, we can easily compute the point on the edge were the fixel makes contact. This is the point where reaction forces will originate. The force is always perpendicular to the edge in contact with the fixel, in the direction of the part interior.
Once the solution is displayed, the user can click anywhere within the part and drag the mouse to a new location to specify a force. The force acts at the point where the user first clicked. The magnitude and direction of the force are indicated by the distance and direction from the click-point to the current mouse location.
This force exerts translation forces on the part in both the X and Y directions, as well as inducing a torque. The fixels will react against this force in the direction normal to the edge. The magnitude of the reaction force at each fixel is dependent on the magnitude and direction of the user-supplied force. In fact, one fixel will have no reaction force at all - i.e. the user force is borne by only three of the fixels.
To compute the magnitude of the reaction forces at each fixel, we solve the following system of equations:
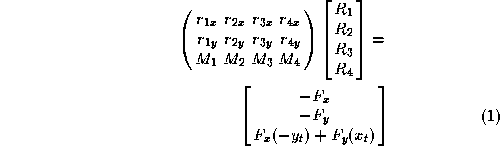
where,
;
is the unit reaction force at fixel i with components
and
;
is the contact point of fixel i with the part edge;
and
are the X and Y components of the user-specified force;
is the location of the user force;
is the magnitude of the reaction force at fixel i.
The first two equations say that the translation forces from the fixels and the user force are balanced - i.e. cancel each other out. The last equation says that the torque induced by the user force is canceled out.
Because this system is over constrained (three equations and four
unknowns), and because we are searching for a solution where one fixel
has zero reaction force, we solve the system four times, each time
setting one of the terms to zero. Our objective is a solution
with non-negative values for the remaining terms; a solution
with a negative magnitude for a reaction force is nonsensical.
Once we have a non-negative solution with at least one term equal to zero, we can use these to compute the lengths of the reaction vectors. We can then draw them normal to the edges, pointing towards the interior of the part.
A sample screen shot showing a part, the fixture and the reaction forces is shown in figure 3. The user-applied force can be see as a line originating at the leftmost vertex of the part and moving down and to the right - i.e. towards the origin of the workspace.
All of these computations and the display of the force vectors take place interactively while the user is dragging the mouse. The computations are performed on the client machine without contacting the FixtureNet server. In fact, it would be very difficult to provide real-time updates if round-trip communication with the server were required. The resulting user interface would probably be very jerky and uneven.
