Hydration and Hydrolysis of Metal Cations

Hydration

When sodium chloride dissolves in water, the sodium and chloride ions and the polar water molecules are strongly attracted to one another by ion-dipole interactions. The solvent molecules (water in this case) surround the ions removing them from the crystal and forming the solution. As the dissolving process proceeds, the individual ions are removed from the solid surface becoming completely separate, hydrated species in the solution.

Dissolution of NaCl in Water

In order to dissolve the sodium chloride in the water, three processes have to occur:
  1. the water molecules must be separated (H-bonds must be broken)
  2. the forces of attraction between the ions in the NaCl lattice must be broken
  3. solute-solvent(ion-dipole)interations must be formed
The overall enthalpy change in forming a solution is the sum of energy changes for each of these processes.



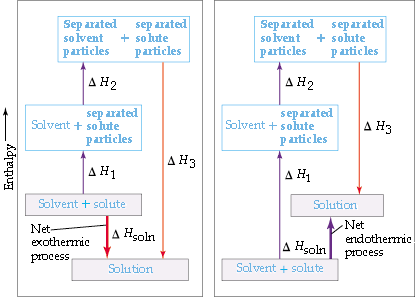
Enthalpy of Solution


Whether the dissolution process will be exothermic or endothermic depends on the relative magnitudes of the energy changes for the three steps. In general, a substance will be insoluble if the energy expended to break apart the solvent and solute particles is significantly greater than the energy given off when solute-solvent interactions are established.

Hydration Energy

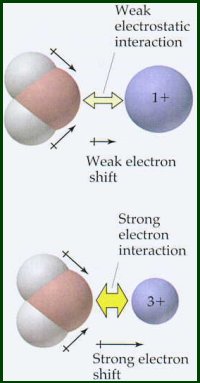
If you were to take gaseous cations and put them into water, they would form hydrated ions and release large amounts of energy. This energy is called the hydration energy of the cation. Although this is an experiment that is impossible to perform, the hydration energies have been determined indirectly (you will see how this is done later in the term).

Click for Table of Hydration Energies


PROBLEMS
  1. Using the data in the Table of Hydration Energies, explain the trends in hydration enthalpies versus ionic radii.

  2. Consider elements of similar charge and radius that have different electronegativity.
    • compare Rb+1 and Tl+1
    • compare Sr+2 and Pb+2
    • compare Lu+3 and Tl+3
    Offer an explanation for the observed trend.




As expected from Coulomb's Law , the hydration energy of a cation depends on the charge and radius of the cation.
Hydration energy also depends on the electronegativity of the element.
Latimer observed that when the electronegativity of the metal is not too great, a good approximation of the hydration energy of a metal ion is given by the following equation:

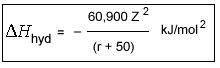Latimer's Equation


In this equation Z is the charge on the cation and r is the cationic radius (in pm). The constant, 50, roughly equates to the radius of the oxygen atom in water.

Latimer's equation does not include the effects of electronegativity. This equation is valid for cations that have electronegativities less than 1.5. Compare the hydration energy data for cations having electronegativities <1.5 and those having electronegativities >1.5. Cations with electronegativies >1.5 have substantially higher hydration energies than more electropositive cations of comparable radius and charge. These electronegative metals have some degree of covalent bonding in their interaction with the oxygen atom of the water molecule, i.e., oxygen's unshared pair of electrons is shared with the metal atom.

Hydrolysis

Metal ions in aqueous solution behave as Lewis acids. The positive charge on the metal ion draws electron density from the O-H bond in the water. This increases the bond's polarity making it easier to break. When the O-H bond breaks, an aqueous proton is released producing an acidic solution.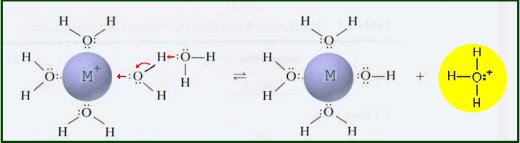
Hydrolysis of a hydrated cation The equilibrium constant for this reaction can be measured.

[M(H2O)n]z+ + H2O [M(H2O)n-1(OH)](z-1)+ + H3O+

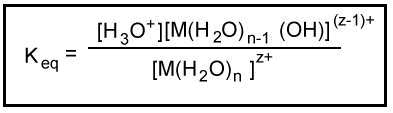
Ka equation

Note the similarity of the equation for the hydrolysis of a hydrated cation with the equation for the ionization of a weak acid in aqueous solution.



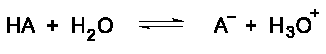
The Keq for the hydrolysis of a hydrated cation is analogous to the Ka for the ionization of a weak acid. Keq is an acid ionization constant. Generally, hydrolysis constants for cations are tabulated as -log Ka. These tabulated hydrolysis constants are averages of different experimental measurements that sometimes differ by more than one pKa unit. For this reason, small differences are not considered significant when comparing the values of these constants.

Click for Table of Hydrolysis Constants


PROBLEMS
Use the data in the Table of Hydrolysis Constants for Metal Cations for these questions.
  1. Consider the ions of Group 2A.
    • What trend exists between ionic radius and the hydrolysis constant?
    • What trend exists between electronegativity and the hydrolysis constant?
  2. Consider Na+1, Ca+2, and Pu+3.
    • What trend exists between ionic charge and hydrolysis?
  3. Offer explanation for the trends that you observe.

  4. Determine a relationship between the charge to radius ratio and metal cation acidity
    • Plot the pKa values as a function of Z2/r for the cations having electronegativities <1.5. Use values from 0 to 0.22 for the x-axis and -4 to 16 for the y-axis. Do a least squares fit of the data.

    • Superimpose acidity categories on your plot and complete the following table.

      Category pKa Range Z2/r Ratio
      non acidic 12-15  
      feebly acidic 11.5-14  
      weakly acidic 6-11.5  
      moderately acidic 1-6  
      strongly acidic (-4)-1  
  5. Determine a relationship between the charge to radius ratio and metal cation acidity for cations of electronegativities >1.5 by plotting pKa versus [Z2/r + 0.096(EN-1.50)] where EN is electronegativity and superimpose acidity categories on your graph.
  6. Compare the two plots. Do you see any trend?